Node 节点 / 结点
父节点 左子节点 右子节点
子节点:直接子节点
度:每一个节点的子节点数量
二叉树
二叉树:任意节点的 度<=2
根节点
根节点的左子树 / 根节点的右子树
二叉查找树 == 二叉排序树 == 二叉搜索树 = Binary search tree
遍历
前序遍历: 中 -> 左 -> 右
中序遍历: 左 -> 中 -> 右 (常见)
后序遍历: 左 -> 右 -> 中
层序遍历: 当前层 -> 下一层
平衡二叉树
特殊的 Binary search tree
任意节点左右子树高度不超过1
旋转机制
触发:当添加一个节点之后 不再是平衡二叉树, 旋转机制 调整
确定支点:从添加的节点开始,往上找
左旋:
支点 -> 左子,
右子 -> 支点,
原右子的左子 -> 新左子的右子
右旋:支点降为右子节点
支点 -> 右子,
左子 -> 支点,
原左子的右子 -> 新右子的左子
添加节点在子树 -> 旋转
左左 -> 右
右右 -> 左
左右 -> 左右
右左 -> 右左
红黑树
最开始叫 平衡二叉B树 ,后来改名
红黑规则:
- 每个 Node 仅是 红色 或 黑色
- 根 Node 必是 黑色
- 最末端的空指针处,为 Nil / 黑Node / 叶Node
主要看后两个规则:
- 两红Node 不能相连
- 每一Node 到其下方的 每一叶Node , 每一路径包含的 黑Node 数相同
添加节点:
默认红色(效率高)
添加节点规则:
预设添加的节点为 Red
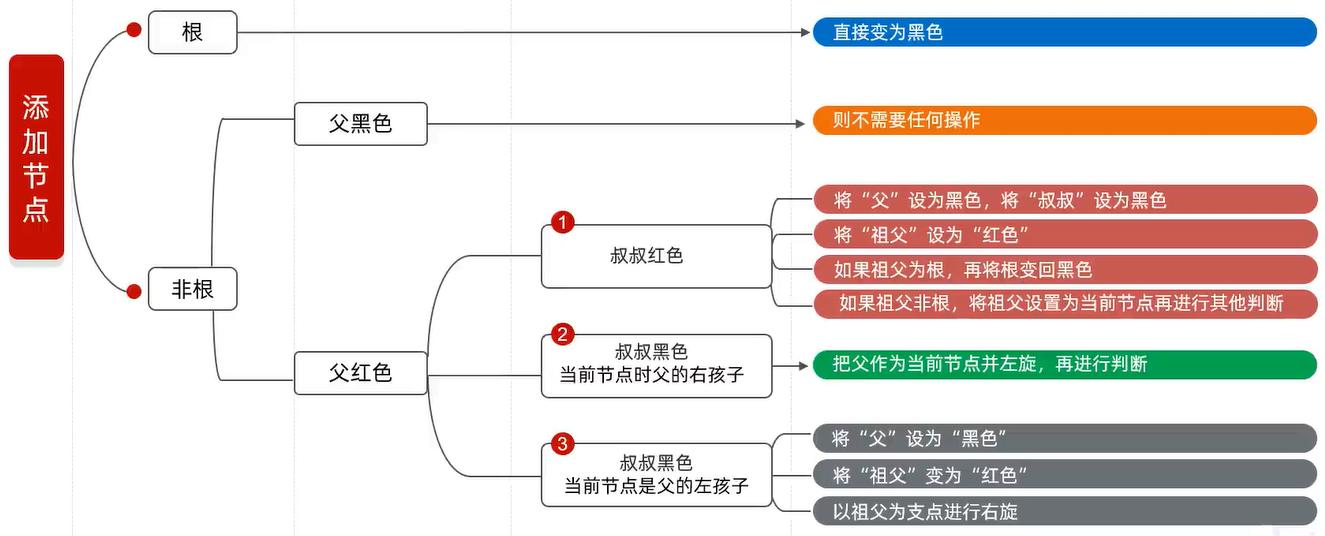
红黑树的增删改查性能较好,因为其旋转次数较少