时间复杂度
局限性
一些数据,如n较小时,不能仅凭时间复杂度判断算法效率的高低。尽管如此,复杂度分析仍然是评判算法效率最有效且常用的方法。
统计方式
忽略掉变化较小的,
类型
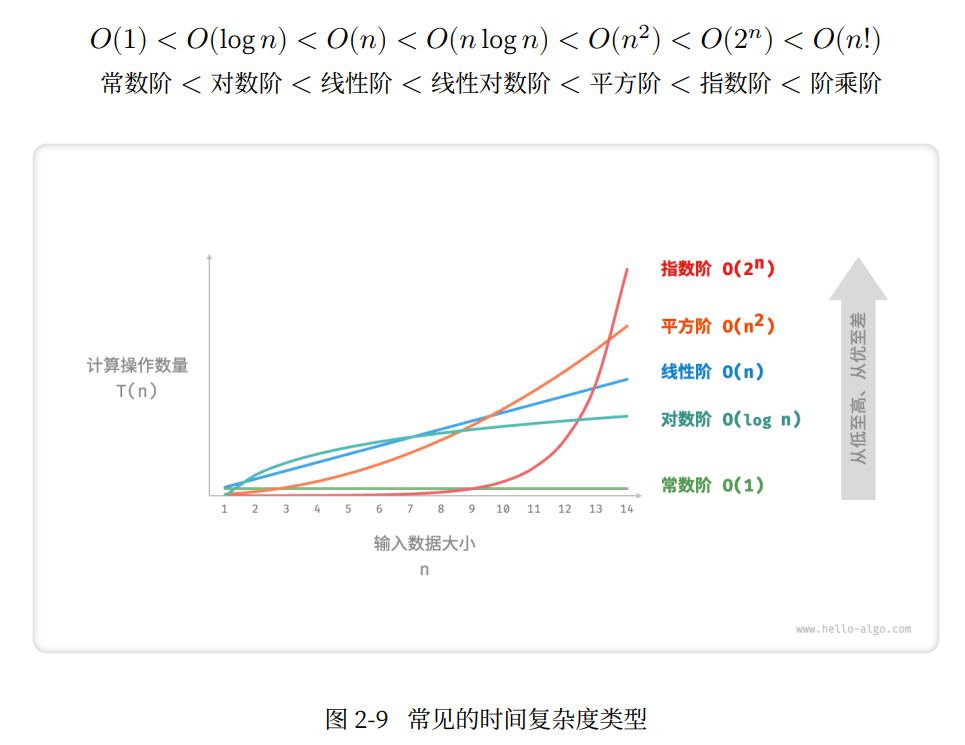
𝑂(1) 常数阶
𝑂(log 𝑛) 对数阶
“每轮缩减到一半”
𝑂(𝑛) 线性阶
𝑂(𝑛 log 𝑛) 线性对数阶
𝑂(𝑛^2) 平方阶
𝑂(2^𝑛) 指数阶
𝑂(𝑛!) 阶乘阶
空间复杂度 space complexity
内存空间分类
- 输入空间。
- 暂存空间:用于存储算法在运行过程中的变量、对象、函数上下文等数据。
- 暂存数据:各种常量、变量、对象等。
- 栈帧空间:调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
- 指令空间:在实际统计中通常忽略不计
- 输出空间
通常统计的是: 暂存数据 + 栈帧空间 + 输出空间
通常只关注最差空间复杂度,因为需要保证所有的数据都能够有足够的空间
常见复杂度类型
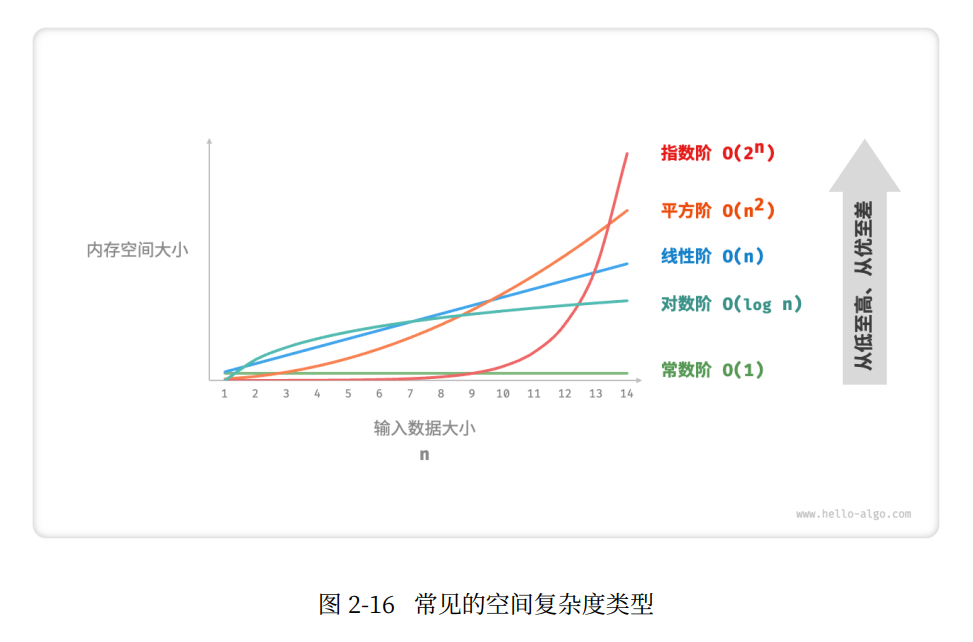
𝑂(1) < 𝑂(log 𝑛) < 𝑂(𝑛) < 𝑂(𝑛^2) < 𝑂(2^𝑛)
尾递归的空间复杂度
理论上,尾递归函数的空间复杂度可以被优化至 𝑂(1) 吗? 𝑂(1) 。不过绝大多数编程语言(例如 Java、Python、C++、Go、C# 等)都不支持自动优化尾递归,因此通常认为空间复杂度是 𝑂(𝑛) 。